Introduction to Quantum Computing – A New Era of Computation
Quantum computing represents a paradigm shift in computational power, harnessing the principles of quantum mechanics to process information in ways fundamentally different from classical computers. Unlike classical bits, which can represent either a 0 or a 1, quantum computers utilize qubits, which can exist in multiple states simultaneously due to a phenomenon called superposition. This unique quantum feature, when paired with entanglement, allows quantum computers to address complex problems at an exponentially faster rate than traditional classical computers. Imagine a coin spinning in the air. Before it lands, it’s neither heads nor tails; it’s both. This is similar to how a qubit exists in multiple states simultaneously. Quantum computers leverage this counterintuitive behavior to explore multiple possibilities at once, offering the potential to revolutionize fields from drug discovery to artificial intelligence.

In the following sections, we will delve deeper into the quantum computing basics, exploring how quantum computing works, its advantages over classical computing, and the industries it is poised to transform.
Understanding the Quantum Leap: Classical vs. Quantum Computing
To fully appreciate the potential of quantum computing, it’s essential to understand how it differs from classical computing. Let’s break down the key distinctions.
Classical vs. Quantum Computing
| Feature | Classical Computing | Quantum Computing |
|---|---|---|
| Basic Unit | Bits (0 or 1) | Qubits (superposition of 0 and 1) |
| Information Processing | Sequential, one operation at a time | Parallel, multiple calculations simultaneously |
| Computational Power | Limited by the number of bits | Exponential growth in power with additional qubits |
| Strengths | Efficient for deterministic calculations, large datasets, complex algorithms | Excels at optimization problems, simulations, and breaking complex codes |
| Limitations | Struggles with certain optimization problems, quantum simulations, and cryptography | Faces challenges in error correction and scalability |
| Use Cases | Data processing, spreadsheets, word processing, traditional software | Drug discovery, materials science, finance, cryptography, AI |
While classical computers have been instrumental in technological advancements, quantum computers promise to tackle problems that are intractable for their classical counterparts. This paradigm shift has the potential to revolutionize various industries and scientific disciplines.
Quantum Computing Principles
Quantum mechanics is a field of physics that explores the behavior of matter and energy on atomic and subatomic scales. Unlike classical mechanics, which governs the motion of macroscopic objects, quantum mechanics deals with the strange and counterintuitive world of the very small.
Superposition
One of the most fundamental concepts in quantum mechanics is superposition. Unlike classical bits, which can only be in one state (0 or 1), a quantum bit, or qubit, can exist in multiple states simultaneously. Imagine a coin spinning in the air. Before it lands, it’s neither heads nor tails; it’s both. This is analogous to a qubit’s state of superposition. In technical terms, a qubit can be in a combination of the |0⟩ and |1⟩ states at the same time, described by a linear combination of these states.
Entanglement
Entanglement is another key concept. When two particles become entangled, their states become interconnected, no matter the distance between them. Measuring the state of one particle immediately defines the state of the other, regardless of the separation. This phenomenon defies classical intuition and is essential for many quantum computing operations. For example, entangled qubits can be used to perform complex calculations simultaneously, providing the foundation for quantum parallelism.
Interference
Interference is the ability of quantum waves to either reinforce or cancel each other out. This principle is fundamental to understanding how quantum computers can process information differently from classical computers. In quantum computing, interference is used to amplify the probability of correct answers and diminish the probability of incorrect ones. This is achieved through the constructive and destructive interference of quantum states, enhancing the efficiency and accuracy of quantum algorithms.
These counterintuitive concepts form the bedrock of quantum mechanics and are essential for understanding how quantum computers operate. In the next section, we will delve into how these principles are applied in the realm of quantum computing, providing a deeper insight into their practical implementation.
The Building Blocks of Quantum Computing
Qubits: The Quantum Equivalent of Classical Bits
Definition and Comparison to Classical Bits
- Classical Bits: In traditional computing, information is stored and processed using bits. Each bit is a binary unit that can be in one of two states: 0 or 1. These bits form the basis of all classical computing operations.
- Qubits: In contrast, quantum computing uses quantum bits or qubits. Unlike classical bits, qubits can exist simultaneously in multiple states due to the principle of superposition. This allows a qubit to be in a state of 0, 1, or simultaneously both 0 and 1.
Superposition: A New Way to Represent Information
- Classical Representation: In classical computing, bits represent a single state at any given time, limiting the amount of information that can be processed simultaneously.
- Quantum Representation: Qubits utilize superposition, allowing them to perform multiple calculations at once. For example, if you have two qubits, they can represent four states simultaneously (00, 01, 10, 11), significantly increasing the computing power.
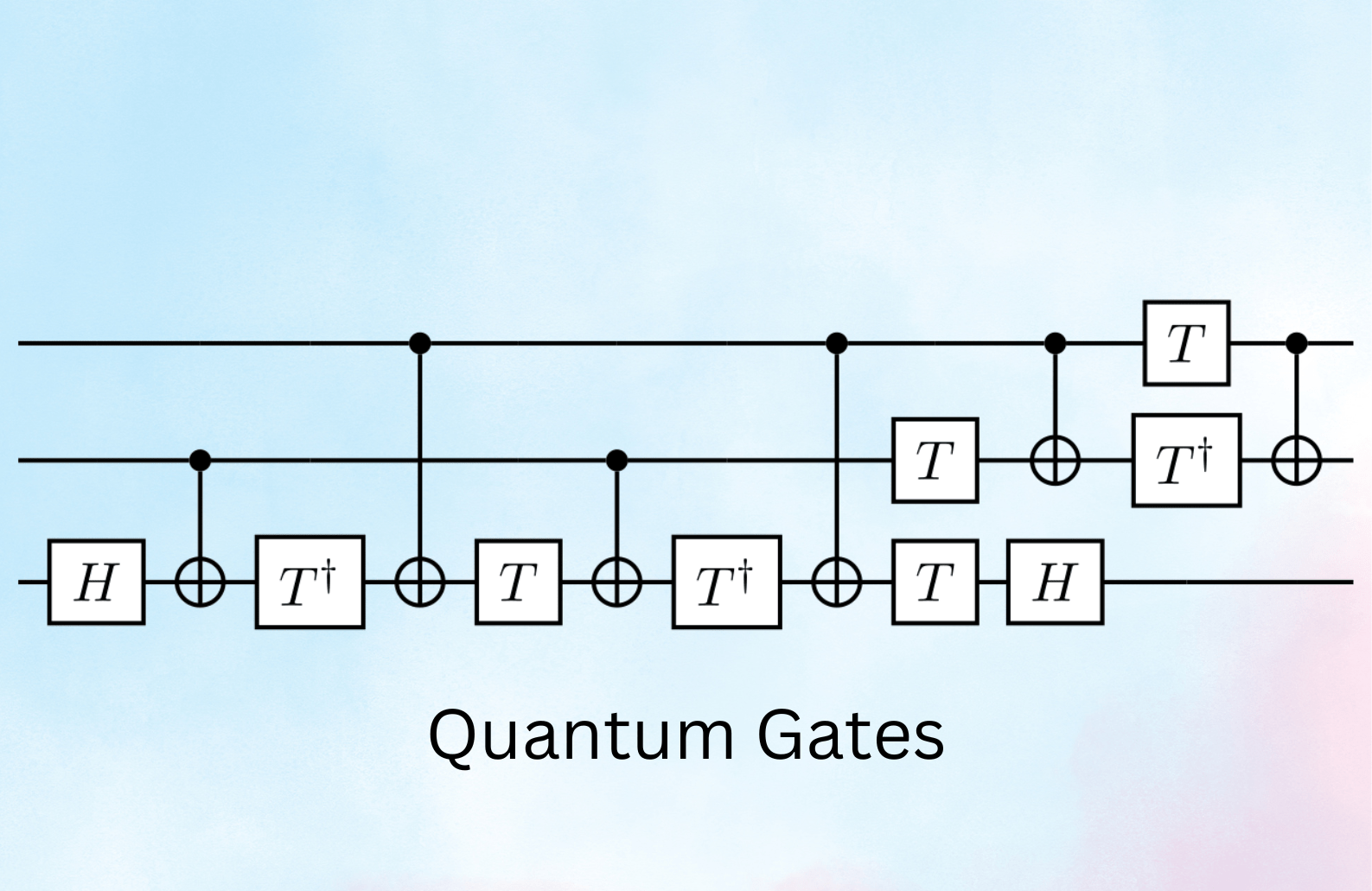
Quantum Gates: Manipulating Qubits
- Definition and Role: Quantum gates are the quantum equivalent of classical logic gates. They are used to manipulate qubits by changing their states. These gates perform operations on qubits through unitary transformations, maintaining the quantum nature of the information.
- Basic Quantum Gates:
In quantum computing, quantum gates are the building blocks of quantum circuits, similar to how classical logic gates are used in traditional computing. These gates manipulate qubits through specific operations, enabling quantum computations. Here are some basic quantum gates and how they work:
Pauli-X Gate (NOT Gate)
- Function: The Pauli-X gate, also known as the NOT gate, flips the state of a qubit. If the qubit is in the state |0⟩, the Pauli-X gate transforms it to |1⟩, and if the qubit is in the state |1⟩, it transforms it to |0⟩.
- Example: Consider a qubit in the state |0⟩. When the Pauli-X gate is applied, it changes to |1⟩. Conversely, if the qubit starts in the state |1⟩, applying the Pauli-X gate flips it to |0⟩. This operation is similar to flipping a bit in classical computing.Hadamard Gate (H Gate)
- Function: The Hadamard gate creates a superposition of states. It takes a qubit in a definite state (|0⟩ or |1⟩) and transforms it into a superposition state, where the qubit has equal probability of being in either state |0⟩ or |1⟩.
- Example: If a qubit is initially in the state |0⟩, applying the Hadamard gate transforms it into the state (|0⟩ + |1⟩) / √2. If the qubit is initially in the state |1⟩, applying the Hadamard gate transforms it into the state (|0⟩ – |1⟩) / √2. This is like taking a coin and spinning it such that it has an equal chance of landing on heads or tails.
CNOT Gate (Controlled NOT Gate)
- Function: The CNOT gate, or Controlled NOT gate, is a two-qubit gate that entangles the states of two qubits. It inverts the state of the second qubit (target qubit) only if the first qubit (control qubit) is in the state |1⟩.
- Example: Suppose you have two qubits, where the first qubit (control) is in the state |1⟩ and the second qubit (target) is in the state |0⟩. Applying the CNOT gate flips the state of the target qubit to |1⟩. If the control qubit is in the state |0⟩, the target qubit remains unchanged. This operation is crucial for creating entangled states, which are necessary for many quantum algorithms.
Combining Quantum Gates
- Building Complex Quantum Circuits: By combining these and other quantum gates, you can construct complex quantum circuits that perform sophisticated computations. For example, quantum algorithms like Shor’s algorithm for factoring large numbers or Grover’s algorithm for database searching leverage the combination of multiple quantum gates to achieve exponential speedup over classical algorithms.
- Example: A simple quantum circuit might involve applying a Hadamard gate to a qubit to create superposition, followed by a CNOT gate to entangle it with another qubit. The resulting entangled state can then be manipulated further using additional gates to perform complex operations. This combination of superposition and entanglement allows quantum computers to process information in ways that classical computers cannot, solving problems exponentially faster.
Understanding these basic quantum gates and how they can be combined is essential for grasping the power and potential of quantum computing. These gates form the foundation upon which all quantum algorithms are built, enabling quantum computers to perform calculations that are currently impossible for classical computers.
Understanding qubits and quantum gates is fundamental to grasping the immense potential of quantum computing. These building blocks enable quantum computers to process vast amounts of information simultaneously, paving the way for breakthroughs in various fields, from cryptography to artificial intelligence.
Quantum Computing Algorithms: How Quantum Computers Solve Problems
Quantum computing algorithms tap into the extraordinary aspects of quantum mechanics, enabling them to solve intricate problems with far greater efficiency compared to classical algorithms.. Here, we introduce two of the most well-known quantum algorithms—Shor’s algorithm and Grover’s algorithm—illustrating how they leverage quantum mechanics to achieve significant computational advantages.
Shor’s Algorithm: Revolutionizing Cryptography
Shor’s algorithm, developed by mathematician Peter Shor in 1994, is designed for factoring large integers, a problem that underpins the security of many cryptographic systems. Classical algorithms struggle with this task, especially as the integers grow larger, making encryption methods like RSA secure under current technology.
How It Works: Shor’s algorithm uses quantum properties such as superposition and entanglement to find the prime factors of a large integer exponentially faster than the best-known classical algorithms. The algorithm involves the following steps:
- Quantum Fourier Transform: A key component of Shor’s algorithm is the quantum Fourier transform (QFT), which helps identify the periodicity in the sequence of numbers. This periodicity is crucial for determining the factors of the integer.
- Modular Exponentiation: The algorithm computes the modular exponentiation, creating a superposition of possible states.
- Measurement and Classical Computation: Finally, the results are measured, and classical computation is used to extract the factors from the periodicity identified by the QFT.
Example: Imagine trying to factor a 2048-bit integer, a task that would take classical computers millions of years. Shor’s algorithm can perform this in a matter of hours on a sufficiently powerful quantum computer. This capability threatens current encryption systems and has spurred the development of quantum-resistant cryptographic methods.
Grover’s Algorithm: Accelerating Database Searches
Grover’s algorithm, introduced by Lov Grover in 1996, offers a quadratic improvement in solving unstructured search problems. Whereas classical methods need O(N) operations to search through an unsorted database of N items, Grover’s algorithm can locate the target item in just O(√N) operations.
How It Works: Grover’s algorithm leverages quantum superposition and interference:
- Superposition: The algorithm begins by placing the quantum system in a superposition of all possible states, representing all items in the database simultaneously.
- Oracle Function: An oracle function is used to mark the correct item by inverting its amplitude.
- Amplitude Amplification: Through a process known as amplitude amplification, the algorithm increases the probability of the correct item being measured.
Example: Consider a database with 1 million entries. A classical search would require, on average, 500,000 checks. Grover’s algorithm can find the desired entry in about 1,000 operations, making it significantly faster for large-scale searches.
Potential Impact of Quantum Computing Algorithms
Cryptography and Security: The ability of Shor’s algorithm to factor large integers efficiently poses a significant threat to current cryptographic systems. This has led to an urgent need to develop quantum-resistant encryption methods to secure sensitive information.
Database Management and Search: Grover’s algorithm’s speedup for search problems can revolutionize fields that rely on large databases, such as data mining, machine learning, and big data analytics. This can lead to faster information retrieval and more efficient data processing.
Optimization and Simulation: Other quantum algorithms are being developed to tackle optimization problems, such as the Quantum Approximate Optimization Algorithm (QAOA), and to simulate quantum systems more accurately, which can advance fields like material science, chemistry, and drug discovery.
By understanding these key quantum algorithms and their potential applications, we can appreciate the transformative power of quantum computing and its potential to revolutionize various industries.
Quantum Hardware: Challenges and Breakthroughs
Technical Challenges in Building Quantum Computers
Building a functional and scalable quantum computer involves overcoming several significant technical challenges:
- Decoherence: Decoherence occurs when a quantum system loses its quantum properties due to interaction with its environment. Maintaining qubits in a coherent state is crucial for reliable quantum computation. Techniques to mitigate decoherence include isolating qubits from environmental noise and using error correction codes.
- Error Correction: Quantum computers are highly susceptible to errors due to decoherence and operational imperfections. Quantum error correction involves encoding qubits into larger quantum systems to detect and correct errors without disturbing the quantum information. This is essential for building fault-tolerant quantum computers.
- Scalability: Scaling up from a few qubits to thousands or millions is a major hurdle. Challenges include maintaining coherence over many qubits, interconnecting them efficiently, and managing the complexity of quantum circuits. Researchers are developing modular quantum computing architectures to address scalability.
Types of Quantum Computers
- Superconducting Qubits: Superconducting qubits use superconducting circuits cooled to cryogenic temperatures to achieve quantum behavior. Companies like IBM and Google use this technology. Superconducting qubits offer fast gate operations and relatively mature fabrication techniques but face challenges with coherence times and scaling.
- Trapped Ion Qubits: Trapped ion quantum computers use ions trapped by electromagnetic fields. Lasers manipulate the ions’ quantum states. Trapped ion systems, such as those developed by IonQ and Honeywell, offer long coherence times and high-fidelity operations but are slower compared to superconducting qubits.
- Photonic Qubits: Photonic quantum computers use light particles (photons) to encode and manipulate quantum information. Photonic systems, like those explored by Xanadu, offer room-temperature operation and easy integration with existing communication infrastructure but face challenges with photon generation and detection.

Recent Breakthroughs in Quantum Computing
The field of quantum computing is rapidly evolving, with new breakthroughs emerging regularly. Here are some of the most significant advancements in recent times:
Error Correction and Stability
- Microsoft’s Qubit Virtualization: Microsoft achieved a major milestone by demonstrating a qubit-virtualization system that performed over 14,000 individual experiments without a single error. This breakthrough marks a significant step towards more reliable quantum computing.
- Google’s Quantum Supremacy: While not without controversy, Google’s claim of achieving “quantum supremacy” in 2019 highlighted the potential of quantum computers to outperform classical supercomputers on specific tasks.
Quantum Hardware Breakthroughs
- Quantum-System-on-Chip (QSoC): Researchers have created a scalable, modular hardware platform that integrates thousands of interconnected qubits on a single chip. This breakthrough advances quantum computing toward real-world applications. Room Temperature Qubits: A team of Japanese researchers created a qubit that can maintain quantum coherence at room temperature, a significant step towards more practical quantum computers.
Quantum Materials
- Quantum Plastics: Researchers have discovered that thin films of elemental bismuth display the non-linear Hall effect at room temperature, opening up new possibilities for quantum materials and devices.
Other Notable Developments
- Quantum Entanglement Over Long Distances: Scientists have successfully entangled photons over increasing distances, bringing us closer to quantum communication networks.
- Quantum Machine Learning: The integration of quantum computing with machine learning is showing promising results in areas like drug discovery and materials science.
These are just a few examples of the rapid progress being made in quantum computing. As research continues, we can expect even more groundbreaking advancements in the near future.
The Future of Quantum Computing
Potential Applications and Industries Revolutionized
- Medicine: Quantum computing can revolutionize drug discovery by simulating molecular interactions with unprecedented accuracy. This could lead to the development of new drugs and treatments for complex diseases.

- Finance: Quantum algorithms can optimize portfolio management, risk analysis, and fraud detection. Financial institutions are exploring quantum computing to gain a competitive edge and enhance decision-making processes.
- Cryptography: Quantum computing poses a threat to current encryption methods but also offers the potential for quantum-resistant cryptography and secure communication through quantum key distribution.
- Artificial Intelligence: Quantum computing can accelerate machine learning algorithms, enabling more efficient training of models and solving complex optimization problems in AI applications.
Ethical Implications and Societal Impact
Quantum computing raises several ethical considerations:
- Data Security: The ability of quantum computers to break current encryption methods poses significant risks to data security and privacy. Developing quantum-resistant encryption is crucial to protect sensitive information.
- Access and Inequality: The high cost and complexity of quantum computing technology may lead to unequal access, potentially widening the gap between technologically advanced and developing regions.
- Job Displacement: As quantum computing automates complex tasks, there may be shifts in the job market. It’s important to consider workforce retraining and education to prepare for these changes.
Future Of Quantum Computing
Imagine a future where quantum computers solve problems previously thought intractable, leading to breakthroughs in medicine, finance, cryptography, and beyond. Quantum computing has the potential to revolutionize industries, drive innovation, and address some of humanity’s most pressing challenges. As we navigate the ethical and societal implications, responsible development and deployment of quantum technologies will be key to realizing this future.
By understanding the challenges, advancements, and potential of quantum hardware, along with the future implications of quantum computing, we can appreciate the transformative power of this technology and its promise to revolutionize various aspects of our lives.
Conclusion
Quantum computing represents a major leap in computational power, leveraging quantum computing principles to process information in fundamentally new ways. Unlike classical systems with binary bits, quantum computers use qubits that can exist in multiple states due to superposition, enabling them to solve complex problems much more efficiently.
Quantum computing algorithms like Shor’s and Grover’s showcase this power, offering solutions to problems that are currently intractable for classical computers. However, significant quantum hardware challenges, such as decoherence and error correction, still need to be overcome. Recent advancements in hardware are making practical quantum computing increasingly attainable.
For a deeper dive into how quantum computers work, their algorithms, and the challenges of quantum hardware, explore our related blogs.